Скажем так по мотивам вот этого - http://18delphi.blogspot.ru/2013/11/blog-post_2.html
И немного вот этого - http://18delphi.blogspot.ru/2013/11/supports.html
Наверное я ещё раз напишу ГЛУПОСТЬ, но похоже - я без этого НЕ МОГУ...
Есть "технари", инженЕры или инженерА... Как кому будет угодно...
И есть - "математики"...
Первых я наблюдаю часто, вторых - "в природе не видел"... За исключением одного-двух, которые реально круты и СОВСЕМ из другого поколения....
Почему я говорю о "закорючках", "ореоле" и попытках усложнения...
Сейчас попробую пояснить...
Есть вот скажем - линейная алгебра - http://ru.wikipedia.org/wiki/%D0%9B%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D0%B0%D1%8F_%D0%B0%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0
Там исследуются вектора и их свойства. Ну а также - матрицы.
Вводятся понятия "векторного пространства". Что это такое. Каким аксиомам должно удовлетворять.
Дальше рассматриваются операции над векторами и матрицами. Всякие разные.
Сложение. Умножение. Транспонирование. Нахождение обратной матрицы.
http://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%80%D0%B0%D1%82%D0%BD%D0%B0%D1%8F_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0
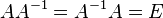
Много всего...
"За лесом - деревьев не видать"...
Ну для меня - "для колхозника"...
Бывают правда преподаватели, которые "могут объяснить на пальцах" сложные вещи.
К счастью я с такими преподавателями - сталкивался.
Не буду называть имён. Может быть я вообще "всё не так понял" и своими ГЛУПОСТЯМИ - запятнаю честное имя хороших преподавателей.
Так вот о чём я?
О "закорючках" и "объяснении на пальцах".
Одна из тем, которая разбирается - это решение системы линейных уравнений и метод Гаусса в частности - http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%93%D0%B0%D1%83%D1%81%D1%81%D0%B0

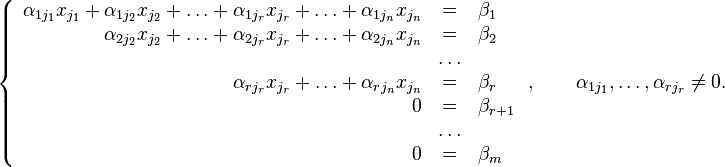
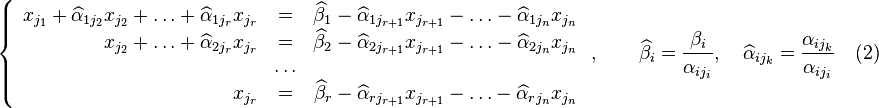 ,
,
где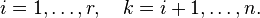
и т.д. и т.п.
Это не так важно...
Это я - худо-бедно постиг....
Так вот что получается "на пальцах"?
Исходная система уравнений преобразуется к виду:
A*x=b
где A - матрица коэффициентов, x - вектор переменных, b - вектор значений.
Что нам это напоминает?
А напоминает нам это - ПРОСТЕЙШЕЕ алгебраическое уравнение:
a*x = b.
Как оно решается?
Да БОЛЕЕ ЧЕМ просто:
x = b/a
Т.е. мы подходим к вопросу, что и система линейных уравнений решается "подобным же образом". А именно:
x = b/A.
Есть только ОДНА незадача. ОПЕРАЦИЯ "деления вектора на матрицу" - НЕ ОПРЕДЕЛЕНА.
Но! Пойдём ДАЛЕЕ в аналогии с алгеброй.
Что такое b/a? Это b*a(в степени -1).
Что такое A(в степени -1)?
Это - МАТРИЦА - ОБРАТНАЯ к A.
Свойства и ПРИНЦИПЫ нахождения которой были ОПРЕДЕЛЕНЫ выше.
Таким образом как решается наша система уравнений? А вот так:
x = b * A(в степени -1)
Вот ТАК объясняют ХОРОШИЕ преподаватели, а не в терминах "скобочек" и "закорючек".
Для инженеров как минимум. Которых - ПОДАВЛЯЮЩЕЕ большинство.
И уж никак не в терминах "свёрток", "сцепок" и прочих вещах из ФЯ, которые я уже забыл.
Мне вот про монады пытались "несколько месяцев объяснить".
Пока я не понял, что "монада" это всего лишь - "конвейер функций". Который сам по себе - недетерминирован, а вот каждая из функций этого конвейера - детерминированна.
(И там - проявлю занудство - можно применять паралеллизм и кеширование результата).
Также хорошие преподаватели "на пальцах" объясняют, "что такое производная".
Что это "с одной стороны" - тангенс угла наклона к кривой графика функции (в каждой точке).
Но! С ДРУГОЙ стороны - ПРОИЗВОДНАЯ это - СКОРОСТЬ. Функция - это пройденный путь - x(t). А производная x'(t) - это скорость. В каждой конкретной точке.
И ОПЯТЬ же - ВСЁ сводится к ГЕОМЕТРИЧЕСКОЙ АНАЛОГИИ.
x'(t0) = (x(t) - (t0))/(t - t0)
Ну и далее говорится примерно следующее - "посмотрите на то как вычисляется "средняя скорость на отрезке времени"".
А вот если отрезок времени устремить к нулю, то получим "реальную скорость в этой точке времени".
Ну примерно такая же аналогия с интегралом и площадью под графиком функции.
И т.д. и т.п.
Даже "дивиргенцию" и "ротор" хорошие преподаватели "ухитряются" объяснить на пальцах.
А уж "градиент" - и подавно.
Ну или скажем - http://ru.wikipedia.org/wiki/%D0%94%D0%B8%D0%BD%D0%B0%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5
Там тоже - "примерно всё понятно"...
"Ключевая идея в динамическом программировании достаточно проста. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико."
Опять наверное скажу ГЛУПОСТЬ, но "хвостовая рекурсия" - по-моему - где-то из этого рода...
Но почему "надо писать закорючки" - не понимаю...
Или вот скажем - "Преобразование Лапласа" - http://ru.wikipedia.org/wiki/%D0%9B%D0%B0%D0%BF%D0%BB%D0%B0%D1%81%D0%B0_%D0%BF%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5
Начинаешь читать статью даже в википедии - "оторопь берёт"...
Но! О чём речь?
В электротехнике мне достаточно доступно это объяснили.
Опять же - для инженеров.
Есть система линейных дифференциальных уравнений. Если я ничего не путаю.
Которая описывает электрическую схему переменного тока с конденсаторами, сопротивлениями и индуктивностями.
Встаёт вопрос - как решить эту систему?
Всё очень просто - переводим систему дифференциальных уравнений, в алгебраическую. Но в КОМПЛЕКСНОЙ плоскости.
Как?
Ребята! Инженеры - для вас есть аналог "таблиц брадиса" и способ "декомпозиции".
Он - ФОРМАЛЬНО описан.
Т.е. ФОРМАЛЬНО из системы дифференциальных уравнений - получаем - систему алгебраических уравнений, в КОМПЛЕКСНОЙ плоскости.
А далее к решению применяем ОБРАТНОЕ преобразование. В виде всё тех же "таблиц Брадиса" и "декомпозиции".
И получаем решение исходной системы.
Всё - "проще некуда"...
Зачем тогда "закорючки", морфизмы и "сцепки"?
Никого не хочу обидеть.
Но! Иногда мне "адепты ФЯ" напоминают "в некотором роде секту". Они влезают в чужие обсуждения" наподобие вот этого - http://18delphi.blogspot.ru/2013/07/blog-post_20.html?showComment=1374677196002#c7262330173032690440 и говорят - "а наш язык - сильно выразительнее".
С ХРЕНА ЛИ он выразительнее, если вы ПОТОМ НЕСКОЛЬКО МЕСЯЦЕВ рассказываете мне про монады? И не можете рассказать.
Хотя - ВСЁ ПРОСТО - http://18delphi.blogspot.ru/2013/11/blog-post_6.html
Почему ГЕНИИ ФЯ - не могли этого СРАЗУ СКАЗАТЬ?
Ну и уж... Рассуждения о "чистых" и "нечистых" ФЯ - http://18delphi.blogspot.ru/2013/11/blog-post_2.html?showComment=1384089384288#c3116006858260631287 - вводит меня в ступор....
РЫБЯТЫ! Простите!
Детерминированность ВАЖНА или нет?
Вот это:
"Функциона́льное программи́рование — раздел дискретной математики и парадигма программирования, в которой процесс вычисления трактуется как вычисление значенийфункций в математическом понимании последних (в отличие от функций как подпрограмм в процедурном программировании).
И немного вот этого - http://18delphi.blogspot.ru/2013/11/supports.html
Наверное я ещё раз напишу ГЛУПОСТЬ, но похоже - я без этого НЕ МОГУ...
Есть "технари", инженЕры или инженерА... Как кому будет угодно...
И есть - "математики"...
Первых я наблюдаю часто, вторых - "в природе не видел"... За исключением одного-двух, которые реально круты и СОВСЕМ из другого поколения....
Почему я говорю о "закорючках", "ореоле" и попытках усложнения...
Сейчас попробую пояснить...
Есть вот скажем - линейная алгебра - http://ru.wikipedia.org/wiki/%D0%9B%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D0%B0%D1%8F_%D0%B0%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0
Там исследуются вектора и их свойства. Ну а также - матрицы.
Вводятся понятия "векторного пространства". Что это такое. Каким аксиомам должно удовлетворять.
Дальше рассматриваются операции над векторами и матрицами. Всякие разные.
Сложение. Умножение. Транспонирование. Нахождение обратной матрицы.
http://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%80%D0%B0%D1%82%D0%BD%D0%B0%D1%8F_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0
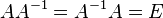
Много всего...
"За лесом - деревьев не видать"...
Ну для меня - "для колхозника"...
Бывают правда преподаватели, которые "могут объяснить на пальцах" сложные вещи.
К счастью я с такими преподавателями - сталкивался.
Не буду называть имён. Может быть я вообще "всё не так понял" и своими ГЛУПОСТЯМИ - запятнаю честное имя хороших преподавателей.
Так вот о чём я?
О "закорючках" и "объяснении на пальцах".
Одна из тем, которая разбирается - это решение системы линейных уравнений и метод Гаусса в частности - http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%93%D0%B0%D1%83%D1%81%D1%81%D0%B0
Пусть исходная система выглядит следующим образом

Матрица  называется основной матрицей системы,
называется основной матрицей системы,  — столбцом свободных членов.
— столбцом свободных членов.
 называется основной матрицей системы,
называется основной матрицей системы,  — столбцом свободных членов.
— столбцом свободных членов.
Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):
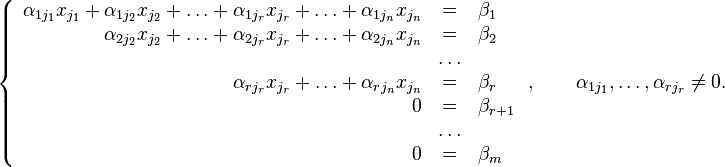
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных  [3].
[3].
 [3].
[3].
Тогда переменные  называются главными переменными. Все остальные называются свободными.
называются главными переменными. Все остальные называются свободными.
 называются главными переменными. Все остальные называются свободными.
называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число 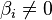 , где
, где 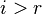 , то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
, то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
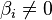 , где
, где 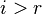 , то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
, то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
Пусть  для любых
для любых 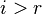 .
.
 для любых
для любых 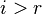 .
.
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом  (
(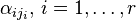 , где
, где  — номер строки):
— номер строки):
 (
(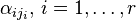 , где
, где  — номер строки):
— номер строки):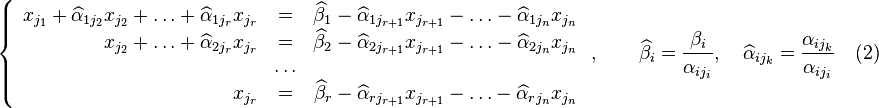 ,
,где
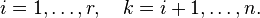
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
и т.д. и т.п.
Это не так важно...
Это я - худо-бедно постиг....
Так вот что получается "на пальцах"?
Исходная система уравнений преобразуется к виду:
A*x=b
где A - матрица коэффициентов, x - вектор переменных, b - вектор значений.
Что нам это напоминает?
А напоминает нам это - ПРОСТЕЙШЕЕ алгебраическое уравнение:
a*x = b.
Как оно решается?
Да БОЛЕЕ ЧЕМ просто:
x = b/a
Т.е. мы подходим к вопросу, что и система линейных уравнений решается "подобным же образом". А именно:
x = b/A.
Есть только ОДНА незадача. ОПЕРАЦИЯ "деления вектора на матрицу" - НЕ ОПРЕДЕЛЕНА.
Но! Пойдём ДАЛЕЕ в аналогии с алгеброй.
Что такое b/a? Это b*a(в степени -1).
Что такое A(в степени -1)?
Это - МАТРИЦА - ОБРАТНАЯ к A.
Свойства и ПРИНЦИПЫ нахождения которой были ОПРЕДЕЛЕНЫ выше.
Таким образом как решается наша система уравнений? А вот так:
x = b * A(в степени -1)
Вот ТАК объясняют ХОРОШИЕ преподаватели, а не в терминах "скобочек" и "закорючек".
Для инженеров как минимум. Которых - ПОДАВЛЯЮЩЕЕ большинство.
И уж никак не в терминах "свёрток", "сцепок" и прочих вещах из ФЯ, которые я уже забыл.
Мне вот про монады пытались "несколько месяцев объяснить".
Пока я не понял, что "монада" это всего лишь - "конвейер функций". Который сам по себе - недетерминирован, а вот каждая из функций этого конвейера - детерминированна.
(И там - проявлю занудство - можно применять паралеллизм и кеширование результата).
Также хорошие преподаватели "на пальцах" объясняют, "что такое производная".
Что это "с одной стороны" - тангенс угла наклона к кривой графика функции (в каждой точке).
Но! С ДРУГОЙ стороны - ПРОИЗВОДНАЯ это - СКОРОСТЬ. Функция - это пройденный путь - x(t). А производная x'(t) - это скорость. В каждой конкретной точке.
И ОПЯТЬ же - ВСЁ сводится к ГЕОМЕТРИЧЕСКОЙ АНАЛОГИИ.
x'(t0) = (x(t) - (t0))/(t - t0)
Ну и далее говорится примерно следующее - "посмотрите на то как вычисляется "средняя скорость на отрезке времени"".
А вот если отрезок времени устремить к нулю, то получим "реальную скорость в этой точке времени".
Ну примерно такая же аналогия с интегралом и площадью под графиком функции.
И т.д. и т.п.
Даже "дивиргенцию" и "ротор" хорошие преподаватели "ухитряются" объяснить на пальцах.
А уж "градиент" - и подавно.
Ну или скажем - http://ru.wikipedia.org/wiki/%D0%94%D0%B8%D0%BD%D0%B0%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5
Там тоже - "примерно всё понятно"...
"Ключевая идея в динамическом программировании достаточно проста. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико."
Опять наверное скажу ГЛУПОСТЬ, но "хвостовая рекурсия" - по-моему - где-то из этого рода...
Но почему "надо писать закорючки" - не понимаю...
Или вот скажем - "Преобразование Лапласа" - http://ru.wikipedia.org/wiki/%D0%9B%D0%B0%D0%BF%D0%BB%D0%B0%D1%81%D0%B0_%D0%BF%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5
Начинаешь читать статью даже в википедии - "оторопь берёт"...
Но! О чём речь?
В электротехнике мне достаточно доступно это объяснили.
Опять же - для инженеров.
Есть система линейных дифференциальных уравнений. Если я ничего не путаю.
Которая описывает электрическую схему переменного тока с конденсаторами, сопротивлениями и индуктивностями.
Встаёт вопрос - как решить эту систему?
Всё очень просто - переводим систему дифференциальных уравнений, в алгебраическую. Но в КОМПЛЕКСНОЙ плоскости.
Как?
Ребята! Инженеры - для вас есть аналог "таблиц брадиса" и способ "декомпозиции".
Он - ФОРМАЛЬНО описан.
Т.е. ФОРМАЛЬНО из системы дифференциальных уравнений - получаем - систему алгебраических уравнений, в КОМПЛЕКСНОЙ плоскости.
А далее к решению применяем ОБРАТНОЕ преобразование. В виде всё тех же "таблиц Брадиса" и "декомпозиции".
И получаем решение исходной системы.
Всё - "проще некуда"...
Зачем тогда "закорючки", морфизмы и "сцепки"?
Никого не хочу обидеть.
Но! Иногда мне "адепты ФЯ" напоминают "в некотором роде секту". Они влезают в чужие обсуждения" наподобие вот этого - http://18delphi.blogspot.ru/2013/07/blog-post_20.html?showComment=1374677196002#c7262330173032690440 и говорят - "а наш язык - сильно выразительнее".
С ХРЕНА ЛИ он выразительнее, если вы ПОТОМ НЕСКОЛЬКО МЕСЯЦЕВ рассказываете мне про монады? И не можете рассказать.
Хотя - ВСЁ ПРОСТО - http://18delphi.blogspot.ru/2013/11/blog-post_6.html
Почему ГЕНИИ ФЯ - не могли этого СРАЗУ СКАЗАТЬ?
Ну и уж... Рассуждения о "чистых" и "нечистых" ФЯ - http://18delphi.blogspot.ru/2013/11/blog-post_2.html?showComment=1384089384288#c3116006858260631287 - вводит меня в ступор....
РЫБЯТЫ! Простите!
Детерминированность ВАЖНА или нет?
Вот это:
"Функциона́льное программи́рование — раздел дискретной математики и парадигма программирования, в которой процесс вычисления трактуется как вычисление значенийфункций в математическом понимании последних (в отличие от функций как подпрограмм в процедурном программировании).
Противопоставляется парадигме императивного программирования, которая описывает процесс вычислений как последовательное изменение состояний (в значении, подобном таковому в теории автоматов). При необходимости, в функциональном программировании вся совокупность последовательных состояний вычислительного процесса представляется явным образом, например как список.
Функциональное программирование предполагает обходиться вычислением результатов функций от исходных данных и результатов других функций, и не предполагает явного хранения состояния программы. Соответственно, не предполагает оно и изменяемость этого состояния (в отличие от императивного, где одной из базовых концепций являетсяпеременная, хранящая своё значение и позволяющая менять его по мере выполнения алгоритма)."
-- УСТОЯВШЕЕСЯ и ОБЩЕПРИНЯТОЕ определение или нет?
Ну и на "закуску".. Опять про линейную алгебру...
Про Евклидово пространство - http://ru.wikipedia.org/wiki/%D0%95%D0%B2%D0%BA%D0%BB%D0%B8%D0%B4%D0%BE%D0%B2%D0%BE_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE
Ну или - метрическое пространство - http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE
"Метри́ческим простра́нством называется множество, в котором определено расстояние между любой парой элементов."
Т.е. ОПРЕДЕЛЕНА - МЕТРИКА.
И если я ПРАВИЛЬНО понимаю - введено скалярное произведение.
И если проводить аналогию то - вектора параллельны, если скалярное произведение равно нулю.
Теперь как определить "похожесть документов"?
Описать документы в виде векторов и ввести метрику... А скалярное произведение - УЖЕ определено...
Если скалярное произведение МЕНЬШЕ какой-то заранее заданной дельты, то документы - "похожи"...
Вопрос конечно только в том - "как ввести метрику"... Но мне лично - это и не сильно интересно...
Я к чему? НА ПАЛЬЦАХ надо всё же стараться объяснять...
Никого не хотел обидеть.
Наверное написал глупость.
P.S. К чему я кстати? "Пишите на Haskell".. "пишите на Python".. РЫБЯТЫ... Обоснуйте! :-) ЗАЧЕМ? МОТИВАЦИЯ какая?
Мне лично - ВООБЩЕ ВСЁ РАВНО на чём программировать.. И да - "Cobol" - уважаю...
P.P.S. что хочу сказать ещё о том как вижу индустрию развития производства ПО - это ТЗ, "чертежи" и тесты. И "номенклатура микросхем". Как-то так "на пальцах"... Ну или "атлас машин и механизмов"...
Ну и - http://ru.wikipedia.org/wiki/%D0%A8%D0%B0%D0%B1%D0%BB%D0%BE%D0%BD%D1%8B_%D0%BF%D1%80%D0%BE%D0%B5%D0%BA%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F
и - http://ru.wikipedia.org/wiki/%D0%90%D0%BB%D0%B5%D0%BA%D1%81%D0%B0%D0%BD%D0%B4%D1%80%D0%B5%D1%81%D0%BA%D1%83,_%D0%90%D0%BD%D0%B4%D1%80%D0%B5%D0%B9
и - http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%B0%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5
P.P.P.S. Вот этого - http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%BD%D1%86%D0%B8%D0%BF_%D0%BC%D0%B0%D0%BA%D1%81%D0%B8%D0%BC%D1%83%D0%BC%D0%B0_%D0%9F%D0%BE%D0%BD%D1%82%D1%80%D1%8F%D0%B3%D0%B8%D0%BD%D0%B0#.D0.9F.D1.80.D0.B8.D0.BD.D1.86.D0.B8.D0.BF_.D0.BC.D0.B0.D0.BA.D1.81.D0.B8.D0.BC.D1.83.D0.BC.D0.B0_.D0.9F.D0.BE.D0.BD.D1.82.D1.80.D1.8F.D0.B3.D0.B8.D0.BD.D0.B0
мне к сожалению "на пальцах" не смогли объяснить...
P.S. К чему я кстати? "Пишите на Haskell".. "пишите на Python".. РЫБЯТЫ... Обоснуйте! :-) ЗАЧЕМ? МОТИВАЦИЯ какая?
Мне лично - ВООБЩЕ ВСЁ РАВНО на чём программировать.. И да - "Cobol" - уважаю...
P.P.S. что хочу сказать ещё о том как вижу индустрию развития производства ПО - это ТЗ, "чертежи" и тесты. И "номенклатура микросхем". Как-то так "на пальцах"... Ну или "атлас машин и механизмов"...
Ну и - http://ru.wikipedia.org/wiki/%D0%A8%D0%B0%D0%B1%D0%BB%D0%BE%D0%BD%D1%8B_%D0%BF%D1%80%D0%BE%D0%B5%D0%BA%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F
и - http://ru.wikipedia.org/wiki/%D0%90%D0%BB%D0%B5%D0%BA%D1%81%D0%B0%D0%BD%D0%B4%D1%80%D0%B5%D1%81%D0%BA%D1%83,_%D0%90%D0%BD%D0%B4%D1%80%D0%B5%D0%B9
и - http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%B0%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5
P.P.P.S. Вот этого - http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%BD%D1%86%D0%B8%D0%BF_%D0%BC%D0%B0%D0%BA%D1%81%D0%B8%D0%BC%D1%83%D0%BC%D0%B0_%D0%9F%D0%BE%D0%BD%D1%82%D1%80%D1%8F%D0%B3%D0%B8%D0%BD%D0%B0#.D0.9F.D1.80.D0.B8.D0.BD.D1.86.D0.B8.D0.BF_.D0.BC.D0.B0.D0.BA.D1.81.D0.B8.D0.BC.D1.83.D0.BC.D0.B0_.D0.9F.D0.BE.D0.BD.D1.82.D1.80.D1.8F.D0.B3.D0.B8.D0.BD.D0.B0
мне к сожалению "на пальцах" не смогли объяснить...
>Вот ТАК объясняют ХОРОШИЕ преподаватели, а не в терминах "скобочек" и "закорючек".
ОтветитьУдалить>И уж никак не в терминах "свёрток", "сцепок" и прочих вещах из ФЯ, которые я уже забыл.
"свёртка" это функция. Одна функция - уже слишком сложно? :D
Изучая новый язык вам в любом случае потребуется изучить новые термины. Вас не должно пугать то, что они здесь похожи на математические. Никакие математические знания не требуются.
>Но! Иногда мне "адепты ФЯ" напоминают "в некотором роде секту".
>Они влезают в чужие обсуждения" наподобие вот этого
Разве я куда-то влезал? До ФП дошло по ходу обсуждения же, нет?
К тому же я подумал, что это интересная тема для обсуждения. И не надо превращать её в "войну". Просто делимся мыслями.
>Хотя - ВСЁ ПРОСТО - http://18delphi.blogspot.ru/2013/11/blog-post_6.html
>Почему ГЕНИИ ФЯ - не могли этого СРАЗУ СКАЗАТЬ?
"ГЕНИИ ФЯ", видимо, думали что вы удосужились таки прочитать хотя-бы определение в вики,
ссылку на которую сами же тогда скинули. Там ровно то же самое написано. >_<
А вообще - вы не с того конца монады начали изучать. Для начала нужно понять сам язык, а в его терминах это не сложнее "интерфейса" с 4мя "методами".
>Ну и уж... Рассуждения о "чистых" и "нечистых" ФЯ
>вводит меня в ступор....
Ещё скажите что мы уже определились с тем, что такое ООП.
"Ещё скажите что мы уже определились с тем, что такое ООП."
Удалить;-)
"
-- Василий Иванович - ты за большевиков али коммунистов?
-- Я - за интернационал!
-- За второй или третий?"
Я ЛИЧНО ни "за" ООП, ни "за" функциональность, ни "за" мультипарадигменность etc
Я - ЗА - "методы решения задач". Удобные и подходящие в каждый конкретный момент.
"думали что вы удосужились таки прочитать хотя-бы определение в вики"
Удалитьсказали грубость, и даже не поняли...
"это интернет детка"...
таки - удосужился...
"Мона́да в функциональном программировании — это *абстракция* линейной цепочки связанных вычислений. Её основное назначение — инкапсуляция функций с побочным эффектом от чистых функций, а точнее их выполнений от вычислений[1]"
Удалить"In functional programming, a monad is a *programming structure* that represents computations. Monads are a kind of *abstract data* type constructor that encapsulate program logic instead of data in the domain model. A defined monad allows the programmer *to chain actions together to build a pipeline* to process data in various steps, in which *each action is decorated with additional processing rules provided by the monad*. Programs written in functional style can make use of monads to structure procedures that include *sequenced operations*, or to define some arbitrary control flows (like handling concurrency, continuations, side effects such as input/output, or exceptions)."
"Функция return описывает «возвращение» (втягивание) типа a в монаду m, то есть обрамление его контейнером."
УдалитьОчень всё понятно :-)
Мне-то - ТЕПЕРЬ - понятно...
""свёртка" это функция. Одна функция - уже слишком сложно?"
УдалитьНе понял..
Я лично знаю только вот такую свёртку - http://ru.wikipedia.org/wiki/%D0%A1%D0%B2%D1%91%D1%80%D1%82%D0%BA%D0%B0_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7)
Удалить>*programming structure*
ОтветитьУдалитьНичего не значит.
>*to chain actions together to build a pipeline*
>*sequenced operations*
"абстракция *линейной цепочки связанных вычислений*". Не то же самое?
>*each action is decorated with additional processing rules provided by the monad*
Непонятно что они хотели этим сказать, и как это могло помочь в понимании.
>Очень всё понятно :-)
>Мне-то - ТЕПЕРЬ - понятно...
Вы, кстати, уверены, что сама "магическая статейка" вам понятна лишь потому, что вы уже знаете о чём речь? Там, к слову, нет ничего про return.
>Не понял..
Свёртка списка. Довольно частая операция, я решил что речь о ней.
>вам понятна лишь потому
ОтветитьУдалитьвам понятна не потому*fix
"Вы, кстати, уверены, что сама "магическая статейка" вам понятна лишь потому, что вы уже знаете о чём речь?"
Удалить-- я думал об этом. Много. НЕ УВЕРЕН.